Pythonでできる単回帰分析｜わかりやすく解説【scikit-learn・散布図付き】

Pythonでデータ分析に挑戦してみたいな。
仕事の数字を自分で読み解けるようになれば、業務改善にもつながるし…転職にも強くなるかもしれない。

でも、こんなことで悩んだことはありませんか？

・単回帰分析って聞くけど、そもそも何をするもの？

・散布図とか相関係数とか…数学っぽくて少し不安…

・エクセルでやれるのは知ってるけど、Pythonでやる意味ってあるの？

・将来は重回帰分析とか機械学習もやりたいけど、どこから始めればいい？

単回帰分析は「データ分析の入口」ですが、実はとてもシンプル。
一度仕組みが分かれば、重回帰分析や機械学習にも自然とつながっていきます。

この記事では、初心者の方でもつまずかないように、単回帰分析とは？からPythonでの実装方法といった基礎の部分を、やさしく解説します。

Pythonを使えば、短いコード数行で直線（回帰直線）が描けてしまいます。
また、コードの使いまわしもできるため、エクセルよりも手軽に感じる人も多いんです。

分析は Jupyter Lab で実行してもOKですし、慣れてきたら Streamlit で分析アプリ化することもできます。

この記事を読み終えるころには、「Pythonで単回帰分析ってこんなに簡単なんだ！」と実感してもらえるはずです。

さあ、一緒に Python × 単回帰分析 でデータ分析の第一歩を踏み出しましょう。

Pythonをしっかり学びたいけれど、「どこから始めたらいいの？」と迷う人は多いと思います。

実は、私も機械学習を勉強し始めた頃はまったく同じで、途中で手が止まってしまうことが何度もありました。

もし、「基礎から順番に、手を動かしながら学びたい」と思うなら、UdemyのPython講座はかなり相性が良いです。

自分の進度に合わせて学べるので、忙しい社会人の方にもおすすめです。

＼ 　機械学習が着実に身につく動画講座はこちら　 ／

Python×機械学習を動画で学びたい方はこちら

単回帰分析とは？初心者でもわかる基本のイメージ

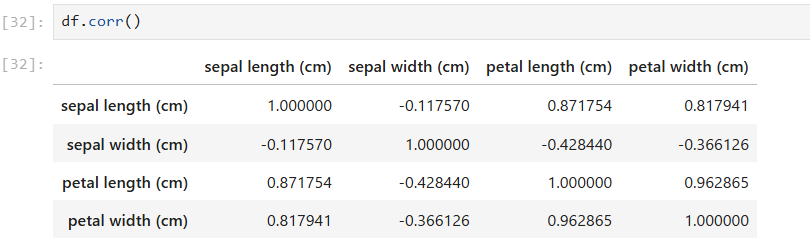
単回帰分析とは、1つの要因（説明変数）が、結果（目的変数）にどれだけ影響しているかを調べる方法のことです。

説明変数＝原因側、目的変数＝結果側、とイメージすると分かりやすいです。

たとえば、こんな関係をイメージすると分かりやすいです。

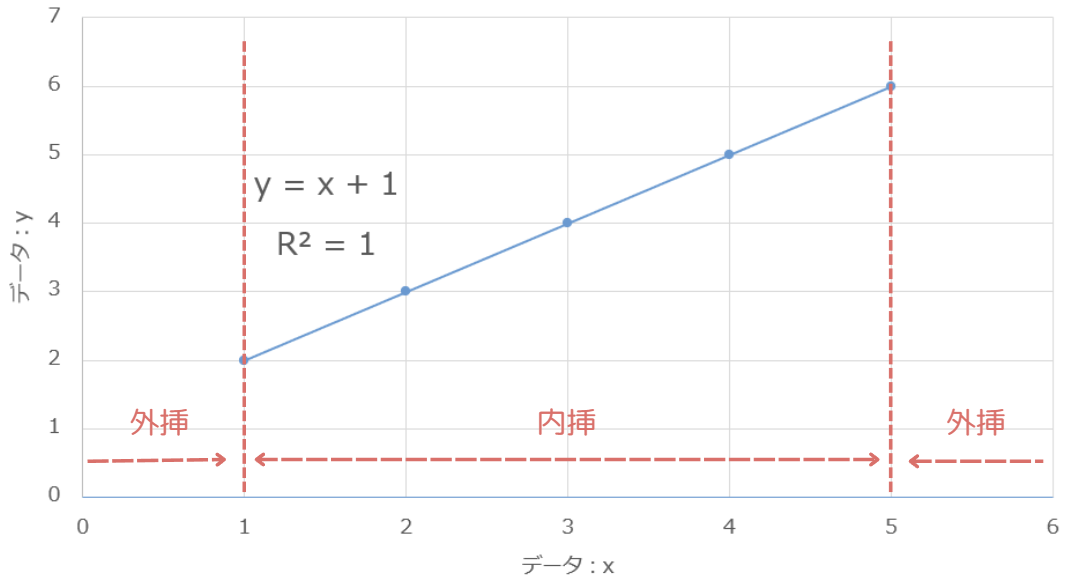
このように、「xが増えると、yはどう変わる？」という関係を調べるときにとても便利なのが単回帰分析です。

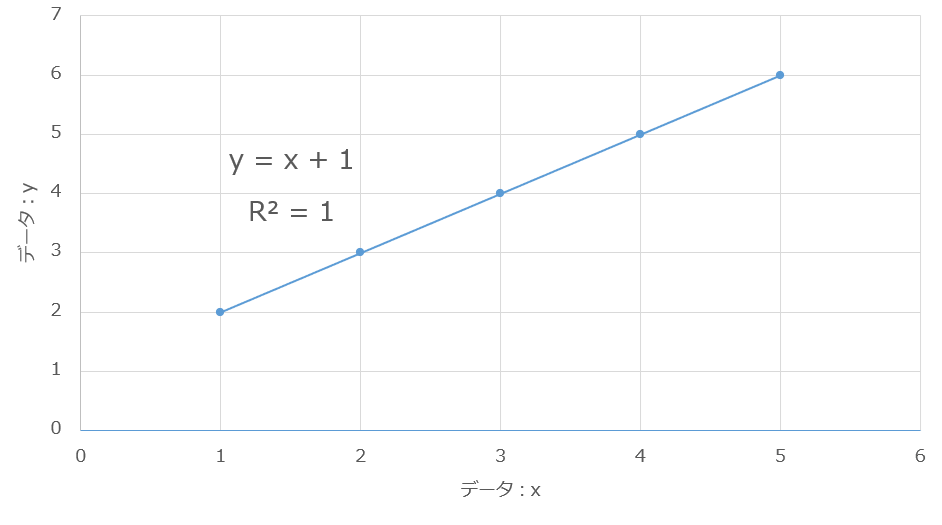
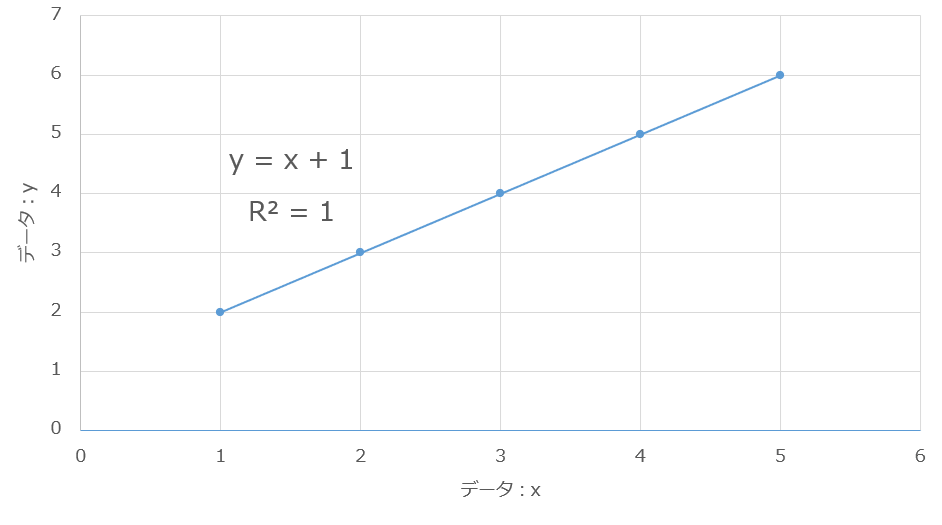
データを散布図でプロットすると点の集まりが見え、その点の流れを最もよく表す直線（回帰直線）を引くのが単回帰分析の基本です。

さらに、この関係の強さを表す指標として使われるのが相関係数（r）と決定係数（r²）です。
これらについては後ほど分かりやすく解説します。

単回帰分析は「説明変数が1つ」の分析ですが、複数になると重回帰分析へ発展します。
どちらも仕組みは同じなので、まずは単回帰分析を理解することが第一歩です。

単回帰分析でよく出てくる用語を簡単に整理しておこう

単回帰分析を理解するうえで、よく耳にする言葉がいくつかあります。
ここでは、最低限だけサラッとまとめておきますね。

Pythonによるあたらしいデータ分析の教科書 第3版 (AI & TECHNOLOGY)

¥3,058 （2025/11/25 17:49時点 | Amazon調べ）

Amazonで探す

楽天市場で探す

Yahooショッピングで探す

ポチップ

散布図とは？

2つの数字の関係を「点」で表したグラフのことです。
点の流れを見ることで、「右肩上がりなのか？」「バラバラなのか？」が分かります。

回帰直線とは？

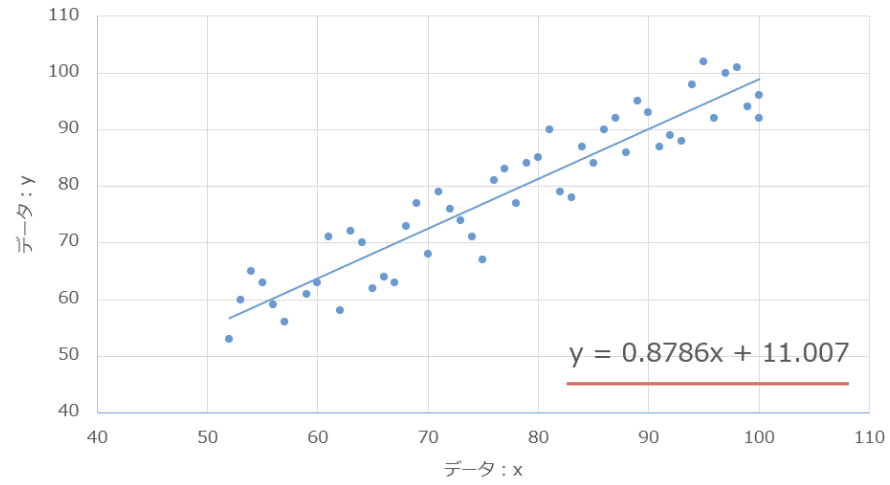
散布図の点の流れを最もよく表す一本の直線のことです。
式で書くと「y = a × x + b」となります。

相関とは？

2つの変数が「どれくらい一緒に動くか」を表す関係性のことです。
「一緒に増えたり」、「どちらかが増えると片方が減ったり…」といった動きの傾向のことになります。

相関係数「r」とは？

相関の強さを「 -1 〜 1 」の数字で表したものです。

エクセルで調べるには「CORREL関数」を使用しましょう。

決定係数 R²（アール二乗）とは？

モデルが「どれくらいデータを説明できているか？」を示す割合です。
「0〜1」の間で表され、数字が大きいほど よく説明できている 状態になります。

ざっくりした目安として「0.7以上」なら
良いモデルとされることが多いです。

Pythonのscikit-learnで単回帰分析を実装してみよう

ここからは、実際にPythonを使って単回帰分析を実装する流れを見ていきましょう。

といっても、難しいコードは一切ありません。
Pythonなら「数行のコード」で単回帰分析が完了します。

Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎

¥3,740 （2025/11/25 17:50時点 | Amazon調べ）

Amazonで探す

楽天市場で探す

Yahooショッピングで探す

ポチップ

今回使うライブラリの紹介（pandas・numpy・scikit-learn・matplotlib）

単回帰分析をPythonで行うとき、よく使われるのが以下の4つです。

① Pandas（パンダス）

表形式のデータを扱うためのライブラリです。
Excelのように「行と列」のデータを扱えるので、初心者でも直感的に理解しやすいのが特徴です。

👉 クリックして、インストール方法を確認する

インストールされているか確認

ターミナル（または Windows の PowerShell）で以下を実行してみましょう。

python -c "import pandas; print(pandas.__version__)"

→ バージョン番号が表示されればインストールされています。
→ エラーが出る場合は未インストールであるため、次のインストールを実行しましょう。

インストール方法

pip install pandas

  詳しく知りたい方は、Pandasの公式ドキュメント「pandas」を見る。

② Numpy（ナムパイ）

数値計算をサポートするライブラリです。
pandas内部でも使われているので、単回帰分析にも自然と登場します。

👉 クリックして、インストール方法を確認する

インストールされているか確認

ターミナル（または Windows の PowerShell）で以下を実行してみましょう。

python -c "import numpy; print(numpy.__version__)"

→ バージョン番号が表示されればインストールされています。
→ エラーが出る場合は未インストールであるため、次のインストールを実行しましょう。

インストール方法

pip install numpy

  詳しく知りたい方は、Numpyの公式ドキュメント「Numpy」を見る。

③ scikit-learn（サイキットラーン）

機械学習の定番ライブラリです。
単回帰分析はもちろん、重回帰分析・決定木・分類モデルなども一通り扱えます。
今回は、単回帰分析用の LinearRegression を使います。

👉 クリックして、インストール方法を確認する

インストールされているか確認

ターミナル（または Windows の PowerShell）で以下を実行してみましょう。

python -c "import sklearn; print(sklearn.__version__)"

→ バージョン番号が表示されればインストールされています。
→ エラーが出る場合は未インストールであるため、次のインストールを実行しましょう。

インストール方法

pip install scikit-learn

  詳しく知りたい方は、scikit-learnの公式ドキュメント「scikit-learn」を見る。

④ matplotlib（マットプロットリブ）

グラフ描画をするためのライブラリです。
散布図や回帰直線の可視化に使います。

👉 クリックして、インストール方法を確認する

インストールされているか確認

ターミナル（または Windows の PowerShell）で以下を実行してみましょう。

python -c "import matplotlib; print(matplotlib.__version__)"

→ バージョン番号が表示されればインストールされています。
→ エラーが出る場合は未インストールであるため、次のインストールを実行しましょう。

インストール方法

pip install matplotlib

pip install japanize-matplotlib

  詳しく知りたい方は、matplotlibの公式ドキュメント「matplotlib」を見る。

Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎

¥3,740 （2025/11/25 17:50時点 | Amazon調べ）

Amazonで探す

楽天市場で探す

Yahooショッピングで探す

ポチップ

それでは実際に単回帰分析を実装してみましょう。

次の4ステップを実行することで単回帰分析ができます。

ここでは、Jupyter labを使用して開発を行っていきますね。

Step1 : 実際にデータを読み込んでみる（Pandas）

まずは、Pandasを使ってデータを読み込みます。
今回は、事前に用意した「XとYのデータ（散布図用）」を使ってみます。

コード

import pandas as pd

# データを用意
df = pd.DataFrame({
    "X": [52,55,57,60,62,64,66,68,70,72,
          74,76,78,80,82,84,86,88,90,92,
          94,96,98,100,54,59,63,67,71,75,
          79,83,87,91,95,99,53,56,61,65,
          69,73,77,81,85,89,93,97,100],
    "Y": [53,63,56,63,58,70,64,73,68,76,
          71,81,77,85,79,87,90,86,93,89,
          98,92,101,96,65,61,72,63,79,67,
          84,78,92,87,102,94,60,59,71,62,
          77,74,83,90,84,95,88,100,92]
})

df.head()

コードの詳細を解説

これで、Excelのように表データとして扱えるようになります。

Step2 : 単回帰分析のモデルを作る（scikit-learn）

いよいよ単回帰分析の設定です。
scikit-learnの LinearRegression クラスを使うことで使用することができます。

コード

from sklearn.linear_model import LinearRegression

# 説明変数と目的変数を準備
X = df[["X"]]  # 2次元の形で渡す
y = df["Y"]

# モデル作成
model = LinearRegression()
model.fit(X, y)

たったこれだけで、単回帰分析の学習が完了します。
すごく簡単ですね！

コードの詳細を解説

Step3 : 回帰係数・切片・R²を確認する

それでは学習が終わったら、結果を確認しましょう。

コード

print("回帰係数（傾き）:", model.coef_[0])
print("切片（b）:", model.intercept_)
print("決定係数 R²:", model.score(X, y))

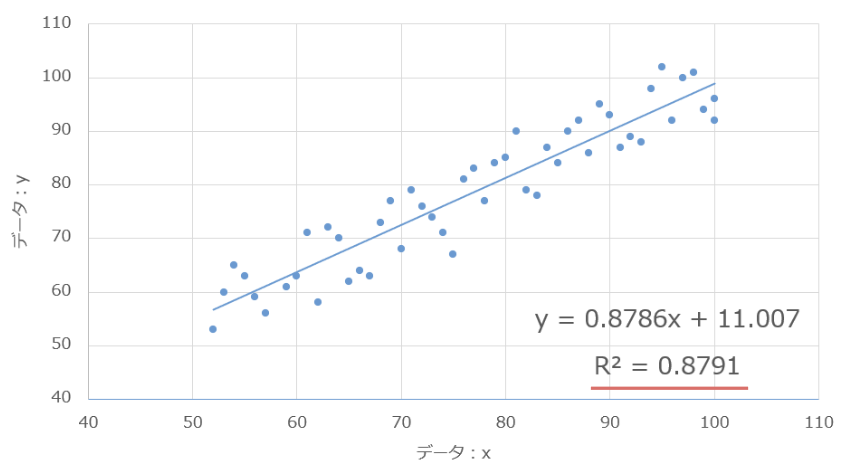
今回のデータは、決定係数が「約0.879」であるため
かなり精度が良いことが分かりますね。

コードの詳細を解説

Step4 : 散布図と回帰直線を描画する（matplotlib）

最後に、散布図と予測したモデルの回帰直線を描いてみましょう。
これがいちばん感動する瞬間です。

コード

import matplotlib.pyplot as plt

y_pred = model.predict(X)  # 予測値を計算

plt.scatter(df["X"], df["Y"], label="データ")  # 散布図
plt.plot(df["X"], y_pred, color="red", label="回帰直線")  # 回帰直線
plt.xlabel("X")  # x軸ラベル
plt.ylabel("Y")  # y軸ラベル
plt.legend()  # 凡例
plt.show()  # グラフ表示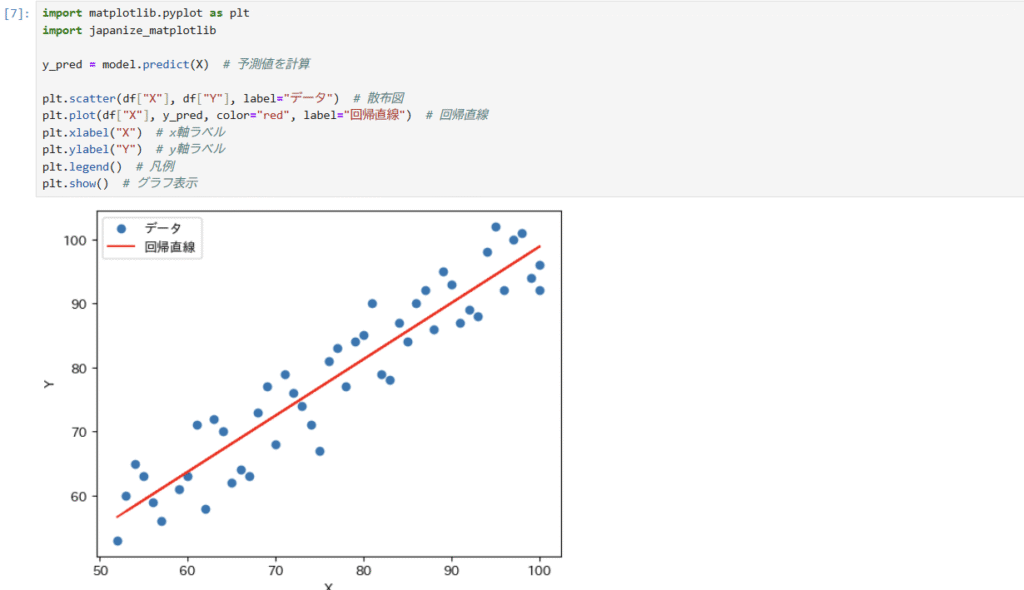

このようにグラフ化することで、分かりやすくなりますよね。

コードの詳細を解説

実行すると、

となり、「単回帰分析とはこういうことか！」と視覚的に理解できます。

単回帰分析でよくある質問（FAQ）まとめ

単回帰分析を始めると、「ここってどう考えたらいいの？」「この場合は単回帰でいいの？」と疑問が出てくると思います。

ここでは、よくあるポイントをサラッと整理しておきますね。

決定係数（R²）が低い場合はどうしたらいい？

単回帰分析で、決定係数（R²）が低い場合は、次の2パターンが多いです。

よくある原因

• 説明変数が1つでは不十分（他の要因が効いている）
• 直線では説明しにくいデータの形をしている

では、どう対処すればいいか？
次の「3つのチェック」を順番にやるだけで原因がつかめます。

やること1 : 相関係数を確認する（df.corr()）

決定係数（R²）は相関係数（r）を2乗した値なので、元の相関が弱いと R²も必然的に低くなります。

Pandas なら、次の1行で全ての目的変数の相関を確認できます。

df.corr()

相関係数の目安

• 0.0〜0.3 → 相関はほぼ弱い
• 0.3〜0.5 → やや弱い
• 0.5〜0.7 → そこそこ関係がある
• 0.7〜1.0 → 強い相関

やること2 : 重回帰分析（説明変数を増やす）

決定係数（R²）が低い原因の多くは「原因が1つでは説明しきれない」ことです。

例えば「売上」を予測したい場合

• 広告費
• 気温
• 商品の種類
• キャンペーンの有無

このような複数の説明変数を入れると、モデルがデータをうまく説明でき、決定係数（R²） が上がりやすくなります。

やること3 : 多項式回帰分析（曲線で表す）

データが直線的でない場合は、「2次関数」「3次関数」… といったような曲線で関係を表す方法（多項式回帰） が有効です。

例えば…

アイスの売上 × 気温なら「気温が上がるほど急激に増える」パターンが多く
直線よりも曲線の方が合うことが多いです。

FAQ一覧に戻る

内挿（interpolation）と外挿（extrapolation）って？

内挿と外挿は、回帰分析ではとても大事な考え方です。

内挿（ないそう）

用意したデータの範囲内で予測することです。
→ 基本的に安全にデータを予測することができます。

例えば…

データが「X=50〜100」なら「X=80」を予測するのは、問題なく予測することができます。

外挿（がいそう）

データの範囲の外を予測することです。
→ 急激に精度が落ちるので注意が必要です。

例えば…

X=50〜100 のデータでX=120 を予測するのは、おすすめしません。

FAQ一覧に戻る

元データはそのまま使っていい？ 欠損値の補完とか必要？

基本的に単回帰分析なら、そのままで問題ありません。
しかし、次のようなデータは事前に前処理を行った方が良いかもしれません。

前処理が必要なケース

• 異常値（外れ値）がある場合
  • 標準偏差を使って外れ値を見つけ、外れ値を処理する
    ※ 削除 or 他の値で置き換え
• 欠損値がある場合
  • pandas のdropna() で削除するか、平均値や中央値で補完する

FAQ一覧に戻る

Pythonで回帰分析をするメリットは？（エクセルと比較）

もちろん エクセルでも単回帰分析は簡単にできます。

ただし Python には次の強みがあります。

Pythonで単回帰分析を行うメリットって？

コードで再現できる（再実行がラク）

一度作ってしまえば、データを変更しても、何度でも同じ分析がすぐできます。

また、散布図＋回帰直線なども数行で作ることもできます。

Plotlyというライブラリを使用してグラフを作成したら、Power BIのように好きなようにグラフを拡大縮小することも可能です。

StreamlitでWebアプリ化できる（最大の強み）

Streamlit を使えば、グラフ作成のコードをWebアプリ化することができます。

Webアプリ化したらこんなに便利です

• ファイルアップロード
• 回帰直線の再計算
• グラフ表示
• 結果の共有

つまり、チームや上司に分析ツールとして配ることも可能です。

FAQ一覧に戻る

まとめ｜Pythonで単回帰分析の第一歩を踏み出そう

この記事では、単回帰分析の基本から、Pythonでの実装方法までを一気に解説しました。

単回帰分析とは「1つの説明変数で結果を予測する方法」で、散布図・回帰直線・相関係数（R）・決定係数（R²）といった基礎を理解することで、データ分析の土台がしっかり身につきます。

また、Pythonを使えば、次のような作業がほぼ数行のコードで可能です。
エクセルよりも再現性が高く、分析の自動化も進めやすいのが特徴です。

さらに今回の「単回帰分析」を理解することで、次のような高度な分析手法へ自然にステップアップできます。

特に、「データ分析を仕事に活かしたい」「転職に向けてスキルを身につけたい」という方にとって、単回帰分析は最初の一歩として最適です。

これからは、ぜひあなた自身のデータで試してみてください。

慣れてきたら、今回書いたコードを、Jupyter Lab や Streamlit に応用し、自作の分析アプリとして社内共有することもできます。

Python × 単回帰分析は、確実にあなたの業務改善に役立つスキルです。
ぜひ次の記事で、より応用的な回帰分析にもチャレンジしてみましょう。

＼ 　自分のペースで学べるPython講座はこちら　 ／

Python未経験でも大丈夫！ Udemyの講座を今すぐチェック

あわせて読みたい

サイトマップ このページは、本サイトの記事を分かりやすくまとめました。ぜひご覧ください。 目次 「共通」を見る 「VBA」を見る 「Officeスクリプト」を見る 「ワークシート関数」...